Method 1: Characteristic curve a(n) in polynomial- or hyperbola form

In the range above the limit speed, the current acceleration is optionally specified by a third-order polynomial or by a hyperbola function. In the case of both characteristics, a constant acceleration a_konst is used in the range below n_grenz. This corresponds to acceleration at nominal speed. The curves apply to both the speed build-up and slow-down phases.

Interpolation points on the drive curve a(n) are used to determine the coefficients of the curves. 4 or 3 interpolation points are required to determine them.

One interpolation point P1=(n_1, (a(n₁)) is already defined by the parameter for constant acceleration a_konst and the limit speed n_grenz and the user can define the remaining 3 or 2 on the drive characteristic a(n). It is best for the abscissa values to be at a constant distance. The equations to determine the coefficients are listed below.

Polynomial

, relative speed

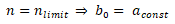
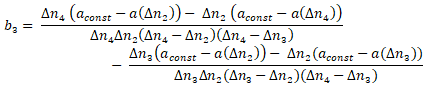
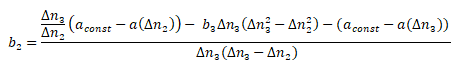
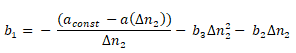
Example of curve determination

a_const = 16000 [°/s²] to n_limit = 12000 [°/s]

The following is obtained for the coefficients:

b3 = -1.92901234E-10 [s/°²]

b2 = 2.08333333E-5 [1/°]

b1 = -0.88888888 [1/s]

b0 = a_konst = 16000 [°/s²]

As from nominal speed (n_limit) the characteristic profile is as follows::

Hyperbola

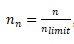, normalised speed,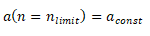

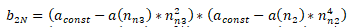
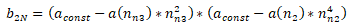
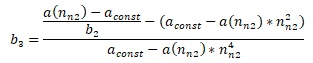
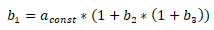
Example of curve determination

A_konst_konst = 16000[degrees/s²] to n_limit = 12000 [degrees/s]

The following is obtained for the coefficients:

b2 = 4.166666E-1[]

b3 = 2.857142E-2[]

b1 = 2.285714E4[°/s²]

As from nominal speed (n_limit) the characteristic profile is as follows::

Parameter

Parameterisation examples

#

beschl_kennlinie.typ         1                 Hyperbola shape

beschl_kennlinie.a_min       1400              [°/s*s]

beschl_kennlinie.n_grenz     12000000          [10-3 °/s]

beschl_kennlinie.a_konst     16000             [°/s*s]

beschl_kennlinie.b1          2.285714E4        [°/s*s]

beschl_kennlinie.b2          4.166666E-1       []

beschl_kennlinie.b3          -2.857142E-2      []

#

#

beschl_kennlinie.typ         2                 Polynomial shape

beschl_kennlinie.a_min       2000              [°/s*s]

beschl_kennlinie.n_grenz     12000000          [10-3 °/s]

beschl_kennlinie.a_konst     16000             [°/s*s]

beschl_kennlinie.b1          -0.88888888       [1/s]

beschl_kennlinie.b2          2.08333333E-5     [1/°]

beschl_kennlinie.b3          -1.92901234E-10   [s/°²]

#