Operating principle

FIR filters (Finite Impulse Response filters) are discrete filters with an impulse response of finite length. These filters have the advantage that they are always stable and so cannot excite themselves to vibrate.

Precisely one of these axis filters can be enabled for each axis and then acts on the setpoint signal of that axis.

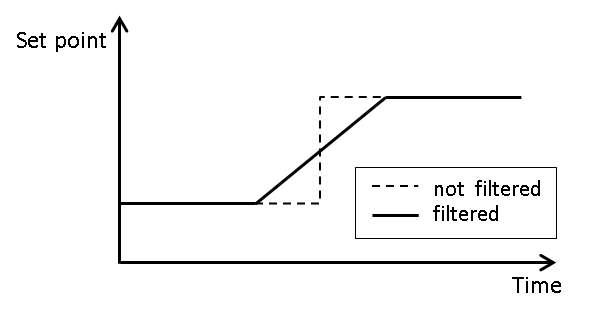
As shown in Figure Step response of axis setpoint filter, filters have a smoothing effect on the filtered signal (here: step response). Depending on the filter used, the signal curve or smoothing has a different characteristic. However, smoothing also causes a deviation from the original setpoint curve.

So, using a filter also entails a certain error or distortion in the axis affected. At corners and curvatures on a programmed contour, such an error may lead to contour deviations.

Refer to the subsection Contour deviation for more information on deviations and how they can be limited.

Notice

Using an axis setpoint filter leads to an axis error compared to the unfiltered setpoint signal

and this results in a contour deviation.